IGNOU BECE-15 Elementary Mathematical Methods in Economics - IGNOU Solved Assignment (Latest)
Get IGNOU BECE-15 Assignments Soft Copy ready for Download in PDF for (July 2021 – January 2022) in English and Hindi Language.
- Helps save time and effort-really well
- Promises Good Marks in Less Time
- Answers that are verified and accurate
- Based on IGNOU Guidelines.
BUY BECE-15 COMBO and Save upto 50%
- Description
- Previous Year Solved Question Papers Included
- Assignments Details
- Assignment Submission End Date
- What's Included
PLEASE MATCH YOUR ASSIGNMENT QUESTIONS ACCORDING TO YOUR SESSION
IGNOU BECE-15 (July 2021 – January 2022) Assignment Questions
A. Long Answer Questions
Answer any two questions.
1. A monopolist faces the demand curve Q = 60 – P/2. The cost function is C = Q2 Find the output that maximises this monopolist’s profits. What are the prices at profits and that output? Find the elasticity of demand at the profit maximizing output.
2. A firm in a perfectly competitive market has the following cost function:
C = 1/3q3 – 5q2 + 30q +10
If the market-clearing price is 6, obtain the profit maximising level of output.
3. Consider the following Macro-Model (Multiplier – Accelerator Interaction):
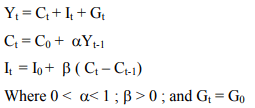
i) Find the time path Y(t) of national income, and
ii) Comment on the stability conditions.
4. Discuss the importance of the Hawkins-Simon conditions in input-output analysis.
B. Medium Answer Questions
Answer any three questions.
5. Using Cramer’s rule solve the following equations:
(i) x + y – 2 = 0
2x- y +2 = 3
4x + 2y -22 = 2
(ii) 2x+4y = 18
4x-6y = 8
6. Find the short run average cost for the production function q = AL1/3K2/3 where total cost (TC) = wL + rK, the symbols having their usual meaning.
7. Find the matrix inverse of
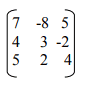
8. Determine the eigenvalues and eigenvectors of the matrix
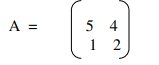
9. i) Let 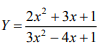
For what values of x will be the function be discontinuous?
ii) Show that 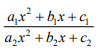
tends to a1/a2 as ![]()
10. Determine the distance between the points:
i) (3, 0, 7) and (- 4, 8, 2)
ii) (4, 6, 7, 1) and (-3, 0, 2, 4)
iii) The distance between the points (3, 1, 2, 4) and ![]() is 200. What can be said about the value of
is 200. What can be said about the value of ![]()
C. Short Answer Questions
Answer any three questions.
11. Evaluate the Limits of
![]()
12. If the demand function for a good is Q= 140 – 5P, what is the price elasticity of demand at P = 15 rupees?
13. If Z = f(x,y) = xy
Find the maximum value for f(x,y) if x & y are constrained to sum to 1 (That is x +y = 1). Solve the problem in two ways: by substitution and by using the Lagrangian multiplier method.
14. Define
a. Adjugate of a matrix
b. Decomposable matrix
c. Singular matrix
15. Determine the characteristic roots and the characteristic vectors of the matrix
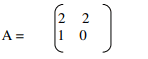
16. Integrate
(i) x Sin x etc.
![]()
IGNOU BECE-15 (July 2020 – January 2021) Assignment Questions
Answer any two questions.
- A monopolist faces the demand curve Q = 80 – P/2. The cost function is C = Q2 Find the output that maximises this monopolist’s profits. What are the prices at profits and that output? Find the elasticity of demand at the profit maximizing output.
- A firm in a perfectly competitive market has the following cost function:
C = 1/3q3 – 5q2 + 30q +30
If the market-clearing price is 9, obtain the profit maximising level of output. - Consider the following Macro-Model (Multiplier – Accelerator Interaction):
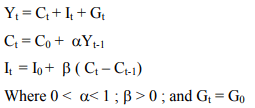
i) Find the time path Y(t) of national income, and
ii) Comment on the stability conditions. - Discuss the importance of the Hawkins-Simon conditions in input-output analysis.
Answer any three questions.
- Using Cramer’s rule solve the following equations:
(i) x + y – 2 = 0
2x- y +2 = 3
4x + 2y -22 = 2
(ii) 2x+4y = 18
4x-6y = 8 - Find the short run average cost for the production function q = AL2/3K1/3 where total cost (TC) = wL + rK, the symbols having their usual meaning.
- Find the matrix inverse of
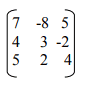
- Determine the eigenvalues and eigenvectors of the matrix
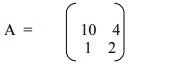
- i) Let
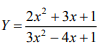
For what values of x will be the function be discontinuous?
ii) Show that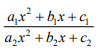
tends to a1/a2 as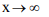
- Determine the distance between the points:
i) (3, 0, 7) and (- 4, 8, 2)
ii) (4, 6, 7, 1) and (-3, 0, 2, 4)
iii) The distance between the points (3, 1, 2, 4) and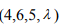 is 200. What can be said about the value of
is 200. What can be said about the value of 
Answer any three questions.
- Evaluate the Limits of
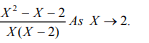
- If the demand function for a good is Q= 280 – 10P, what is the price elasticity of demand at P = 30 rupees?
- If Z = f(x,y) = xy
Find the maximum value for f(x,y) if x & y are constrained to sum to 1 (That is x +y = 1). Solve the problem in two ways: by substitution and by using the Lagrangian multiplier method. - Define
a. Adjugate of a matrix
b. Decomposable matrix
c. Singular matrix - Determine the characteristic roots and the characteristic vectors of the matrix
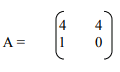
- Integrate
(i) x Sin x
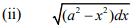
IGNOU BECE-15 (July 2021 – January 2022) Assignment Questions






IGNOU BECE-15 (July 2020 – January 2021) Assignment Questions






BECE-15 Assignments Details
| University | : | IGNOU (Indira Gandhi National Open University) |
| Title | : | Elementary Mathematical Methods in Economics |
| Language(s) | : | English, Hindi |
| Code | : | BECE-15 |
| Degree | : | |
| Subject | : | Mathematics |
| Course | : | Core Courses (CC) |
| Author | : | Gullybaba.com Panel |
| Publisher | : | Gullybaba Publishing House Pvt. Ltd. |









